Acertijo 11

Un pastor, quiere pasar un perro, una oveja y una berza de una a otra orilla de un río. Dispone para ello de una barca en la que solo caben él y una de las otras tres "cosas". Si el perro, se queda solo con la oveja, se la come. Si la oveja se queda sola con la berza, se la come. ¿Cómo debe proceder el pastor?

Acertijo10, el primero después de semana santa

Tenemos 9 bolas, una de las cuáles pesa menos que el resto. Averiguar cuál es utilizando una balanza de dos platillos la menor cantidad de veces posible.

Acertijo 8 (01/02/2012)

El cocido: Dos amigos se disponen a preparar un cocido. Para ello Antonio echó al puchero 200 gramos de garbanzos y Benito aportó 300 gramos. Cuando estuvo preparado apareció Carlos y le invitaron a comer. Al marcharse Carlos les entregó 50 euros para que se los repartieran del modo más justo posible. ¿Cómo lo hicieron?

Acertijo 7 (el primero de febrero)

Hay gatos en un cajón, cada gato en un rincón, cada gato ve tres gatos ¿sabes cuántos gatos son?

Acertijo 6

Acomode todas las piezas de la figura de modo de formar un cuadrado. Las piezas pueden rotarse.

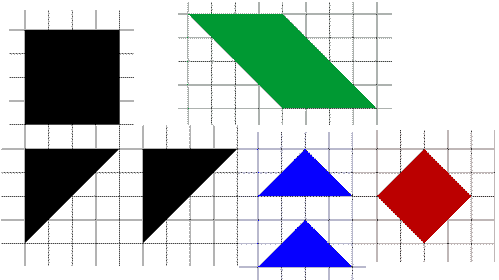
¡Y DEMUESTRAME QUE TÚ PUEDES SIN COPIARLO DE INTERNET!

Solución del Acertijo 5

El ultimo de la fila puede ver el color del sombrero de sus compañeros, si no puede saber cual es el color del suyo es porque los otros dos no son blancos, por lo que o son los dos negros o es uno de cada color.

El segundo de la fila puede ver el color del sombrero del primero y ya ha deducido lo que penso el tercero, si tampoco responde a la pregunta es porque ve que el color del primero es negro, si fuera blanco sabría que el suyo es negro.

El primero por ese mismo planteamiento deduce que su sombrero es negro.

Solución del Acertijo "La Lápida de Diofanto"

A ver cuántos habéis conseguido resolverlo!

Diofanto, vivió 84 años. (  x/6 + x/12 + x/7 + 5 + x/2 + 4 = x )

Solución del Acertijo 4

 PAR
+ RAS
-------------
 ASSA

Solución:
Sabemos que A = 1 (La suma de dos números de 3 cifras siempre es menos que 2000)
A partir de aquí hacemos la suposición de que S + R = 11 y deducimos:
S = 3, R = 8, y P = 5
2. Otro para principiantes:

   IS + SO -------------  SOS

Solución

   91 + 10 -------------  101

La Lápida de Diofanto

Se cuenta que en la lápida de Diofanto, el gran matemático de la Antigüedad que estudió las ecuaciones que llevan su nombre, había la siguiente inscripción:

"Larga fue la vida de Diofanto, cuya sexta parte constituyó su hermosa infancia; su mentón cubrióse de vello después de otro doceavo de su vida; la séptima parte de su vida transcurrió en un matrimonio estéril; pasó un quinquenio más y le nació un hijo, cuya vida sólo duró la mitad de la de su padre, que sólo sobrevivió cuatro años  a la de su amado hijo."

Más tiempo para el Acertijo 4

Hola todos
Voy a dar algo más de tiempo para el Acertijo 4 ya que son muy pocos los que han conseguido resolverlo.
Venga ánimo que vosotros/as podéis!!!!

Acertijo 5 (27-11-2011)

En una mesa hay tres sombreros negros y dos blancos. Tres señores en fila india se ponen un sombrero al azar cada uno y sin mirar el color.

Se le pregunta al tercero de la fila, que puede ver el color del sombrero del segundo y el primero, si puede decir el color de su sombrero, a lo que responde negativamente.

Se le pregunta al segundo que ve solo el sombrero del primero y tampoco puede responder a la pregunta.

Por ultimo el primero de la fila que no ve ningún sombrero responde acertadamente de que color es el sombrero que tenia puesto.

¿Cuál es este color y cual es la lógica que uso para saberlo?

Solución del Acertijo 3

Josefina cumple años el 31 de diciembre. El 30 de diciembre “antes de ayer” tenia 17 , ya que cuando se presenta el enunciado es 1 de enero. Entoces para ese mismo año cumplirá 19 y el proximo 20.

Acertijo 4 (18-11-2011)

Criptogramas numéricos

Los criptogramas numéricos son operaciones de cálculo en las cuales se han sustituido las cifras por letras u otros símbolos de manera que se propone encontrar que valor corresponde a cada letra, teniendo en cuenta, claro, que una misma letra no puede representar dos valores numéricos diferentes. Su resolución, a menudo, exige muchas hipótesis y largos cálculos que implican grandes riesgos de confución.
Las reglas para resolver los criptogramas son las siguientes:

• Los números están en base diez, a menos que se especifique lo contrario.
• Cada letra o símbolo representa un único número.
• El primer dígito de un número no puede ser el cero.

A continuación os propongo unos cuantos criptogramas para que practiqueis.

   PAR + RAS = ASSA

   IS + SO  =  SOS

Solución del Acertijo 2

Una de las posibles soluciones es la siguiente, pero ha habido gente que me ha presentado otras opciones igualmente válidas. De hecho Anastasia ha presentado 8 posibilidades para este cuadro mágico.


Sólo había que comprobar que todas las horizontales, verticales y diagonales sumasen 24 y que los 9 números consecutivos utilizados no se repitiesen.

11      6       7

 4       8       12

 9      10       5

Acertijo 3 (13-11-2011)

Antes de ayer Josefina tenía 17 años, el año que viene tendrá 20.
¿Cómo puede ser?

Solución del Acertijo 1

Bueno chic@s, me alegra deciros que sois geniales, ya que la mayoría de vosotros/as habéis dado la respuesta correcta.

Efectivamente se trataba de dejar encendido el primer interruptor un rato, apagarlo y encender el segundo. Abrir la puerta de la habitación y :

1. Si la luz está encendida era el segundo interruptor
2. Si está apagada, pero la bombilla está caliente, el interruptor bueno es el primero.
3. Y si la luz está apagada, el interruptor es el tercero.

Quiero dar la enhorabuena a los que habéis acertado y animar a los que no lo han hecho a seguir participando. Kilian los interruptores se pueden colocar en paralelo, ya te lo explicaré mañana en clase. He notado que algunas personas que normalmente participan en estos juegos,  no lo han hecho, me gustaría que en el segundo acertijo lo intentasen.

Acertijo 2 (04-11-2011)

        Los cuadrados mágicos son ordenaciones de números en celdas formando un cuadrado, de tal modo que la suma de cada una de sus filas, de cada una de sus columnas y de cada una de sus diagonales dé el mismo resultado.

       El origen de los cuadrados mágicos es muy antiguo. Los chinos y los indios los conocían antes del comienzo de la era cristiana.

       Los cuadrados mágicos se clasifican de acuerdo con el número de celdas que tiene cada fila o columna. Así, uno con 5 celdas se dice que es de quinto orden. No existen cuadrados mágicos de orden 2.

       Aunque todos los matemáticos han reconocido siempre la falta de aplicaciones de los cuadrados mágicos, algunos se han ocupado de ellos con mucha atención: el mérito y gracia del juego está en su insospechada dificultad.

        Coloca nueve números consecutivos en un cuadrado de 3x3, de manera que la suma de las filas y la de las columnas sea 24.

¡ÁNIMO TU PUEDES CONSEGUIRLO!

Acertijo 1 (21-10-2011)

Un hombre esta al principio de un largo pasillo que tiene tres interruptores, al final hay una habitación con la puerta cerrada. Uno de estos tres interruptores enciende la luz de esa habitación, que esta inicialmente apagada.

¿Cómo lo hizo para conocer que interruptor enciende la luz recorriendo una sola vez el trayecto del pasillo?
Pista: El hombre tiene una linterna.

(Tenéis para resolverlo hasta el viernes que viene)

RINCÓN DE LA LÓGICA

Hola a todo@s

Hoy vamos a inagurar esta nueva sección en el Blog educativo de matemáticas. Cada semana colgaré un acertijo, serie o juego matemático, la primera persona que lo resuelva de forma correcta recibirá un punto, y así sucesivamente. Al final del trimestre se contarán las puntuaciones y los que queden en los tres primeros lugares tendrán una bonificación (subida) de la nota y a un premio.

Ánimo y jugar!!!!